Convection Equations
 From Encyclopediaofmath
From Encyclopediaofmath Consider a fluid flow in a layer of uniform depth where the temperature difference,  , between the upper and lower bounding planes is kept constant. Such a system has a steady-state solution in which there is no fluid motion and the temperature varies linearly. If this solution is unstable, convection should develop. When all motion is parallel to the
, between the upper and lower bounding planes is kept constant. Such a system has a steady-state solution in which there is no fluid motion and the temperature varies linearly. If this solution is unstable, convection should develop. When all motion is parallel to the  -plane, the governing equations are [a1]:
-plane, the governing equations are [a1]:
 |
 |
where  is the height of the layer (in the
is the height of the layer (in the  -direction),
-direction),
 |
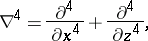 |
 |
stands for the Jacobian determinant,  is a stream function for the two-dimensional fluid motion, and
is a stream function for the two-dimensional fluid motion, and  is the deviation of the temperature from the case where no convection occurs. The coefficients
is the deviation of the temperature from the case where no convection occurs. The coefficients  ,
, 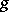 ,
,  ,
,  are, respectively, kinematic viscosity, gravity acceleration, thermal expansion, and thermal conductivity. The part of the first equation that does not depend upon
are, respectively, kinematic viscosity, gravity acceleration, thermal expansion, and thermal conductivity. The part of the first equation that does not depend upon  is the third component of the vorticity equation
is the third component of the vorticity equation
 |
where  is the velocity vector and
is the velocity vector and  is the vorticity.
is the vorticity.
See [a4], [a5], and also Curl and Vector product.
By expanding  and
and 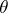 in double Fourier series with coefficients depending on
in double Fourier series with coefficients depending on 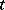 and truncating to three terms, the Lorenz equations result [a2].
and truncating to three terms, the Lorenz equations result [a2].
References[edit]
| [a1] | B. Saltzman, "Finite amplitude free convection as an initial value problem. I" J. Atmos. Sci. , 19 (1962) pp. 329–341 |
| [a2] | E.N. Lorenz, "Deterministic non-periodic flow" J. Atmos. Sci. , 20 (1963) pp. 130–141 |
| [a3] | G.K. Batchelor, "An introduction to fluid dynamics" , Cambridge Univ. Press (1967) |
| [a4] | B.K. Shivamoggi, "Theoretical fluid dynamics" , Martinus Nijhoff (1985) pp. 13–14 |
| [a5] | "Modern developments in fluid dynamics" S. Goldstein (ed.) , Dover, reprint (1965) pp. 114 |
↧ Download as ZWI file | Last modified: 01/11/2026 06:34:11 | 12 views
☰ Source: https://encyclopediaofmath.org/wiki/Convection_equations | License: CC BY-SA 3.0
 KSF
KSF