List Of Graphs

From Handwiki
Short description: none


Individual graphs

  • Balaban 10-cage

  • Balaban 11-cage

  • Bidiakis cube

  • Brinkmann graph

  • Bull graph

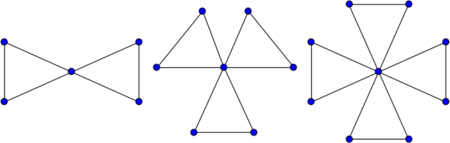
  • Butterfly graph

  • Chvátal graph

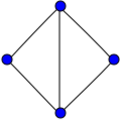
  • Diamond graph

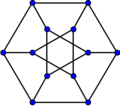
  • Dürer graph

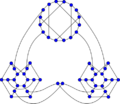
  • Ellingham–Horton 54-graph

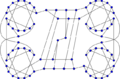
  • Ellingham–Horton 78-graph

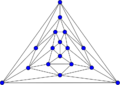
  • Errera graph

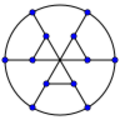
  • Franklin graph

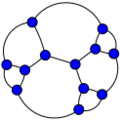
  • Frucht graph

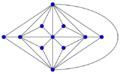
  • Goldner–Harary graph

  • Golomb graph

  • Grötzsch graph

  • Harries graph

  • Harries–Wong graph

  • Herschel graph

  • Hoffman graph

  • Holt graph

  • Horton graph

  • Kittell graph

  • Markström graph

  • McGee graph

  • Meredith graph

  • Moser spindle

  • Sousselier graph

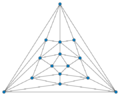
  • Poussin graph

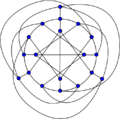
  • Robertson graph

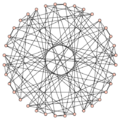
  • Sylvester graph

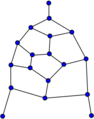
  • Tutte's fragment

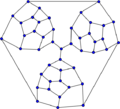
  • Tutte graph

  • Young–Fibonacci graph

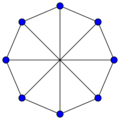
  • Wagner graph

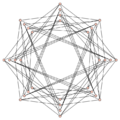
  • Wells graph

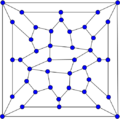
  • Wiener–Araya graph

  • Windmill graph

Highly symmetric graphs

Strongly regular graphs

The strongly regular graph on v vertices and rank k is usually denoted srg(v,k,λ,μ).

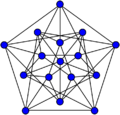
  • Clebsch graph

  • Cameron graph

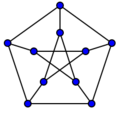
  • Petersen graph

  • Hall–Janko graph

  • Hoffman–Singleton graph

  • Higman–Sims graph

  • Paley graph of order 13

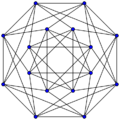
  • Shrikhande graph

  • Schläfli graph

  • Brouwer–Haemers graph

  • Local McLaughlin graph

  • Perkel graph

  • Gewirtz graph

Symmetric graphs

A symmetric graph is one in which there is a symmetry (graph automorphism) taking any ordered pair of adjacent vertices to any other ordered pair; the Foster census lists all small symmetric 3-regular graphs. Every strongly regular graph is symmetric, but not vice versa.

  • Heawood graph

  • Möbius–Kantor graph

  • Pappus graph

  • Desargues graph

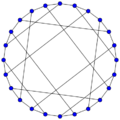
  • Nauru graph

  • Coxeter graph

  • Tutte–Coxeter graph

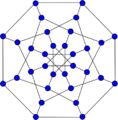
  • Dyck graph

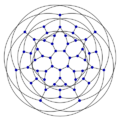
  • Klein graph

  • Foster graph

  • Biggs–Smith graph

  • The Rado graph

Semi-symmetric graphs

  • Folkman graph

  • Gray graph

  • Ljubljana graph

  • Tutte 12-cage

Graph families

Complete graphs

The complete graph on [math]\displaystyle{ n }[/math] vertices is often called the [math]\displaystyle{ n }[/math]-clique and usually denoted [math]\displaystyle{ K_n }[/math], from German komplett.[1]

  • [math]\displaystyle{ K_1 }[/math]

  • [math]\displaystyle{ K_2 }[/math]

  • [math]\displaystyle{ K_3 }[/math]

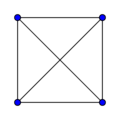
  • [math]\displaystyle{ K_4 }[/math]

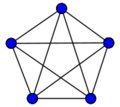
  • [math]\displaystyle{ K_5 }[/math]

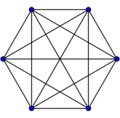
  • [math]\displaystyle{ K_6 }[/math]

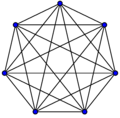
  • [math]\displaystyle{ K_7 }[/math]

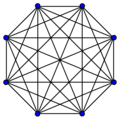
  • [math]\displaystyle{ K_8 }[/math]

Complete bipartite graphs

The complete bipartite graph is usually denoted [math]\displaystyle{ K_{n,m} }[/math]. For [math]\displaystyle{ n=1 }[/math] see the section on star graphs. The graph [math]\displaystyle{ K_{2,2} }[/math] equals the 4-cycle [math]\displaystyle{ C_4 }[/math] (the square) introduced below.

  • [math]\displaystyle{ K_{2,3} }[/math]

  • [math]\displaystyle{ K_{3,3} }[/math], the utility graph

  • [math]\displaystyle{ K_{2,4} }[/math]

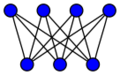
  • [math]\displaystyle{ K_{3,4} }[/math]

Cycles

The cycle graph on [math]\displaystyle{ n }[/math] vertices is called the n-cycle and usually denoted [math]\displaystyle{ C_n }[/math]. It is also called a cyclic graph, a polygon or the n-gon. Special cases are the triangle [math]\displaystyle{ C_3 }[/math], the square [math]\displaystyle{ C_4 }[/math], and then several with Greek naming pentagon [math]\displaystyle{ C_5 }[/math], hexagon [math]\displaystyle{ C_6 }[/math], etc.

  • [math]\displaystyle{ C_3 }[/math]

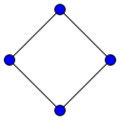
  • [math]\displaystyle{ C_4 }[/math]

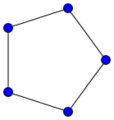
  • [math]\displaystyle{ C_5 }[/math]

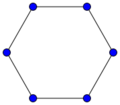
  • [math]\displaystyle{ C_6 }[/math]

Friendship graphs

The friendship graph Fn can be constructed by joining n copies of the cycle graph C3 with a common vertex.[2]

The friendship graphs F2, F3 and F4.

Fullerene graphs

In graph theory, the term fullerene refers to any 3-regular, planar graph with all faces of size 5 or 6 (including the external face). It follows from Euler's polyhedron formula, V – E + F = 2 (where V, E, F indicate the number of vertices, edges, and faces), that there are exactly 12 pentagons in a fullerene and h = V/2 – 10 hexagons. Therefore V = 20 + 2h; E = 30 + 3h. Fullerene graphs are the Schlegel representations of the corresponding fullerene compounds.

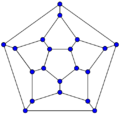
  • 20-fullerene (dodecahedral graph)

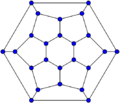
  • 24-fullerene (Hexagonal truncated trapezohedron graph)

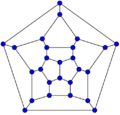
  • 26-fullerene graph

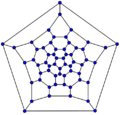
  • 60-fullerene (truncated icosahedral graph)

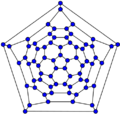
  • 70-fullerene

An algorithm to generate all the non-isomorphic fullerenes with a given number of hexagonal faces has been developed by G. Brinkmann and A. Dress.[3] G. Brinkmann also provided a freely available implementation, called fullgen.

Platonic solids

The complete graph on four vertices forms the skeleton of the tetrahedron, and more generally the complete graphs form skeletons of simplices. The hypercube graphs are also skeletons of higher-dimensional regular polytopes.

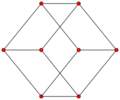
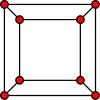
  • Cube
    [math]\displaystyle{ n=8 }[/math], [math]\displaystyle{ m=12 }[/math]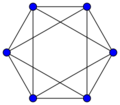

  • Octahedron
    [math]\displaystyle{ n=6 }[/math], [math]\displaystyle{ m=12 }[/math]

  • Dodecahedron
    [math]\displaystyle{ n=20 }[/math], [math]\displaystyle{ m=30 }[/math]

  • Icosahedron
    [math]\displaystyle{ n=12 }[/math], [math]\displaystyle{ m=30 }[/math]

Truncated solids

  • Truncated tetrahedron

  • Truncated cube

  • Truncated octahedron

  • Truncated dodecahedron

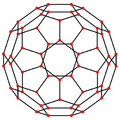
  • Truncated icosahedron

Snarks

A snark is a bridgeless cubic graph that requires four colors in any proper edge coloring. The smallest snark is the Petersen graph, already listed above.

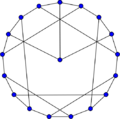
  • Blanuša snark (first)

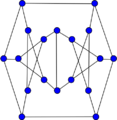
  • Blanuša snark (second)

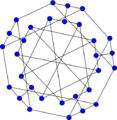
  • Double-star snark

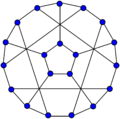
  • Flower snark

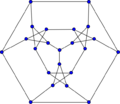
  • Loupekine snark (first)

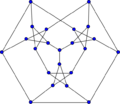
  • Loupekine snark (second)

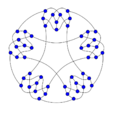
  • Szekeres snark

  • Tietze graph

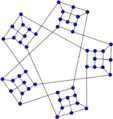
  • Watkins snark

Star

A star Sk is the complete bipartite graph K1,k. The star S3 is called the claw graph.

The star graphs S3, S4, S5 and S6.

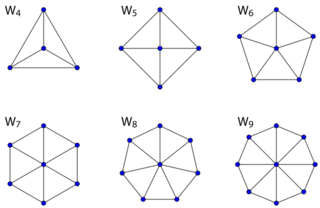
Wheel graphs

The wheel graph Wn is a graph on n vertices constructed by connecting a single vertex to every vertex in an (n − 1)-cycle.

Wheels [math]\displaystyle{ W_4 }[/math] – [math]\displaystyle{ W_9 }[/math].

Other graphs

This partial list contains definitions of graphs and graph families which are known by particular names, but do not have a Wikipedia article of their own.

Gear

G4

A gear graph, denoted Gn, is a graph obtained by inserting an extra vertex between each pair of adjacent vertices on the perimeter of a wheel graph Wn. Thus, Gn has 2n+1 vertices and 3n edges.[4] Gear graphs are examples of squaregraphs, and play a key role in the forbidden graph characterization of squaregraphs.[5] Gear graphs are also known as cogwheels and bipartite wheels.

Helm

A helm graph, denoted Hn, is a graph obtained by attaching a single edge and node to each node of the outer circuit of a wheel graph Wn.[6][7]

Lobster

A lobster graph is a tree in which all the vertices are within distance 2 of a central path.[8][9] Compare caterpillar.

Web

The web graph W4,2 is a cube.

The web graph Wn,r is a graph consisting of r concentric copies of the cycle graph Cn, with corresponding vertices connected by "spokes". Thus Wn,1 is the same graph as Cn, and Wn,2 is a prism.

A web graph has also been defined as a prism graph Yn+1, 3, with the edges of the outer cycle removed.[7][10]

References

  1. ↑ David Gries and Fred B. Schneider, A Logical Approach to Discrete Math, Springer, 1993, p 436.
  2. ↑ Gallian, J. A. "Dynamic Survey DS6: Graph Labeling." Electronic Journal of Combinatorics, DS6, 1-58, January 3, 2007. [1] .
  3. ↑ Brinkmann, Gunnar; Dress, Andreas W.M (1997). "A Constructive Enumeration of Fullerenes". Journal of Algorithms 23 (2): 345–358. doi:10.1006/jagm.1996.0806. 
  4. ↑ Weisstein, Eric W.. "Gear graph". http://mathworld.wolfram.com/GearGraph.html. 
  5. ↑ Bandelt, H.-J.; Chepoi, V.; Eppstein, D. (2010), "Combinatorics and geometry of finite and infinite squaregraphs", SIAM Journal on Discrete Mathematics 24 (4): 1399–1440, doi:10.1137/090760301 
  6. ↑ Weisstein, Eric W.. "Helm graph". http://mathworld.wolfram.com/HelmGraph.html. 
  7. ↑ 7.0 7.1 "Archived copy". http://www.combinatorics.org/Surveys/ds6.pdf. 
  8. ↑ "Google Discussiegroepen". http://groups.google.com/groups?selm=Pine.LNX.4.44.0303310019440.1408-100000@eva117.cs.ualberta.ca. Retrieved 2014-02-05. 
  9. ↑ Weisstein, Eric W.. "Lobster". http://mathworld.wolfram.com/Lobster.html. 
  10. ↑ Weisstein, Eric W.. "Web graph". http://mathworld.wolfram.com/WebGraph.html. 



Retrieved from "https://handwiki.org/wiki/index.php?title=List_of_graphs&oldid=3431415"

Categories: [Mathematics-related lists] [Graphs] [Graph families]

↧ Download as ZWI file | Last modified: 08/05/2024 09:30:21 | 4 views
☰ Source: https://handwiki.org/wiki/List_of_graphs | License: CC BY-SA 3.0

✘
ZWI is not signed. [what is this?]

ZWI viewer by the EncyclosphereKSF