Quasi-Random Graph

In graph theory, there are several notions as to what it means for a sequence of graphs to be "random-like". Roughly speaking, we would like to call a sequence of graphs "random-like" if certain graph properties of the sequence are reasonably similar to those of a sequence of Erdős–Rényi random graphs. In the late 1980s, Fan Chung, Ronald Graham and Richard Wilson showed that many of the notions are in fact equivalent.

Statement

Let [math]\displaystyle{ p\in(0,1) }[/math] be a fixed constant, and let [math]\displaystyle{ \{G_n\}_{n=1}^{\infty} }[/math] be a sequence of graphs with [math]\displaystyle{ \{G_n\} }[/math] having [math]\displaystyle{ n }[/math] vertices and [math]\displaystyle{ (p+o(1))\binom{n}{2} }[/math] edges, for fixed [math]\displaystyle{ 0\lt p\lt 1 }[/math]. Denote [math]\displaystyle{ G_n }[/math] by [math]\displaystyle{ G }[/math]. Then, the following graph properties are equivalent:

1. (Discrepancy condition): [math]\displaystyle{ |e(X,Y)-p|X||Y||=o(n^2) }[/math] for all vertex sets [math]\displaystyle{ X,Y\subset V(G) }[/math].
2. (Alternative discrepancy condition): [math]\displaystyle{ \left|e(X)-p\binom{|X|}{2}\right|=o(n^2) }[/math] for all vertex set [math]\displaystyle{ X\subset V(G) }[/math].
3. (Graph counting condition): For each graph [math]\displaystyle{ H }[/math], the number of labelled copies of [math]\displaystyle{ H }[/math] in [math]\displaystyle{ G }[/math] (i.e. vertices in [math]\displaystyle{ H }[/math] are distinguished) is [math]\displaystyle{ (p^{e(H)}+o(1))n^{v(H)} }[/math]. The [math]\displaystyle{ o(1) }[/math] term may depend on [math]\displaystyle{ H }[/math].
4. (4-cycle counting condition): The number of labelled copies of [math]\displaystyle{ C_4 }[/math] is at most [math]\displaystyle{ (p^4+o(1))n^4 }[/math].
5. (Codegree condition): Let [math]\displaystyle{ \operatorname{codeg}(u,v) }[/math] denote the number of common neighbors of two vertices [math]\displaystyle{ u }[/math] and [math]\displaystyle{ v }[/math] in [math]\displaystyle{ G }[/math]. Then, [math]\displaystyle{ \sum_{u,v\in V(G)} |\operatorname{codeg}(u,v)-p^2n|=o(n^3) }[/math].
6. (Eigenvalue condition): If [math]\displaystyle{ \lambda_1\ge \lambda_2\ge\cdots\ge\lambda_{v(G)} }[/math] are the eigenvalues of the adjacency matrix of [math]\displaystyle{ G }[/math], then [math]\displaystyle{ \lambda_1=pn+o(n) }[/math] and [math]\displaystyle{ \max_{i\neq 1} |\lambda_i|=o(n) }[/math].

If any of the above conditions is satisfied, then we say that the sequence of graphs [math]\displaystyle{ \{G_n\}_{n=1}^{\infty} }[/math] is quasi-random.

Sketch of proof

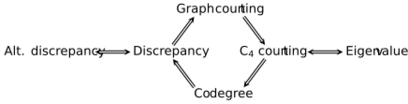
In what follows, [math]\displaystyle{ v(H)=|V(H)| }[/math] and [math]\displaystyle{ e(H)=|E(H)| }[/math].

Discrepancy condition [math]\displaystyle{ \implies }[/math] Alternative discrepancy condition.

Simply take [math]\displaystyle{ Y=X }[/math].

Alternative discrepancy condition [math]\displaystyle{ \implies }[/math] Discrepancy condition.

By the inclusion–exclusion principle, we can write [math]\displaystyle{ e(X,Y) }[/math] in terms of the edge counts of individual vertex sets: [math]\displaystyle{ e(X,Y)=e(X\cup Y)+e(X\cap Y)-e(X\setminus Y)-e(Y\setminus X). }[/math] Then, by the alternative discrepancy condition,

[math]\displaystyle{ p\left(\binom{|X\cup Y|}{2}+ \binom{|X\cap Y|}{2} + \binom{|X\setminus Y|}{2}+\binom{|Y\setminus X|}{2} + o(n^2) \right) = p|X||Y| + o(n^2). }[/math]

Discrepancy condition [math]\displaystyle{ \implies }[/math] Graph counting condition

This follows from the graph counting lemma, taking [math]\displaystyle{ V_i=G }[/math] for [math]\displaystyle{ i=1,\ldots,v(H) }[/math].

Graph counting condition [math]\displaystyle{ \implies }[/math] 4-cycle counting condition

The 4-cycle [math]\displaystyle{ C_4 }[/math] is just a special case of [math]\displaystyle{ H }[/math].

4-cycle counting condition [math]\displaystyle{ \implies }[/math] Codegree condition

Using the idea of the second moment method from probabilistic combinatorics, we can show that the variance of [math]\displaystyle{ \operatorname{codeg}(u,v) }[/math] is [math]\displaystyle{ o\left(n^3\right) }[/math].

Codegree condition [math]\displaystyle{ \implies }[/math] Discrepancy condition

This follows from Cauchy-Schwarz and the definition of codegree.

Eigenvalue condition [math]\displaystyle{ \implies }[/math] 4-cycle counting condition

The number of labelled 4-cycles in [math]\displaystyle{ G_n }[/math] is within [math]\displaystyle{ O(n^3) }[/math] of the number of closed walks of length 4 in [math]\displaystyle{ G_n }[/math], which is [math]\displaystyle{ \operatorname{tr}(A_G^4) }[/math], where [math]\displaystyle{ A_G }[/math] denote the adjacency matrix of [math]\displaystyle{ G }[/math]. From linear algebra, we know that [math]\displaystyle{ \operatorname{tr}(A_G^4)=\sum_{i=1}^n \lambda_i^4 }[/math]. The dominating term is [math]\displaystyle{ \lambda_1 }[/math]: by assumption, [math]\displaystyle{ \lambda_1^4=p^4n^4+o(n^4) }[/math]. It remains to check that the sum of the other [math]\displaystyle{ \lambda_i^4 }[/math]s are not too big. Indeed, [math]\displaystyle{ \sum_{i\ge 2}\lambda_i^4\le\max_{i\neq 2}|\lambda_i|^2\sum_{i\ge 1}\lambda_i^2=\max_{i\neq 2}|\lambda_i|^2\operatorname{tr}(A_G^2)=\max_{i\neq 2}|\lambda_i|^2\cdot2e(G)=o(n^4). }[/math]

4-cycle counting condition [math]\displaystyle{ \implies }[/math] Eigenvalue condition

By the min-max theorem, [math]\displaystyle{ \lambda_1\ge \frac{\boldsymbol{1}^TA_G\boldsymbol{1}}{\boldsymbol{1}^T\boldsymbol{1}}=\frac{2e(G)}{n}=\left(p+o(1)\right)n }[/math], where [math]\displaystyle{ \boldsymbol{1} }[/math] denote the vector in [math]\displaystyle{ \mathbb{R}^{v(G)} }[/math] whose entries are all 1. On the other hand, by the 4-cycle counting condition [math]\displaystyle{ \lambda_1^4\le \sum_{i=1}^n \lambda_i^4=\operatorname{tr} A_G^4\le p^4n^4+o(n^4). }[/math]Thus, [math]\displaystyle{ \lambda_1= pn+o(n) }[/math], and [math]\displaystyle{ \max_{i\neq 1} |\lambda_i|^4\le \operatorname{tr}(A_G^4)-\lambda_1^4\le p^4n^4-p^4n^4+o(n^4)=o(n^4). }[/math]

References

• Chung, F. R. K.; Graham, R. L.; Wilson, R. M. (February 1988). "Quasi-random graphs". Proceedings of the National Academy of Sciences of the United States of America 85: 969–970. doi:10.1073/pnas.85.4.969. PMID 16593909. 
• Chung, F. R. K.; Graham, R. L.; Wilson, R. M. (December 1989). "Quasi-random graphs". Combinatorica 9: 345–362. doi:10.1007/BF02125347. 
• Thomason, Andrew (1987). "Pseudorandom graphs". Random graphs '85 (Poznań, 1985). North-Holland Math. Stud.. 144. North-Holland, Amsterdam. pp. 307–331. 
• Thomason, Andrew (1987). "Random graphs, strongly regular graphs and pseudorandom graphs". Surveys in combinatorics 1987 (New Cross, 1987). London Math. Soc. Lecture Note Ser.. 123. Cambridge Univ. Press, Cambridge. pp. 173–195. 
• Zhao, Yufei. "Graph Theory and Additive Combinatorics" (PDF). pp. 71–76. http://yufeizhao.com/gtac/fa17/gtac.pdf. 

0.00 (0 votes)