Pendulum
 From Conservapedia
From Conservapedia 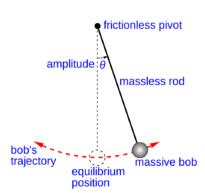
A pendulum is an object that is suspended from a pivot and allowed to swing.[1] Pendula are particular useful for making clocks as they have a regular period when they oscillate. The mass at the end of the pendulum is known as the "bob".
Contents
- 1 History
- 2 Physics of Pendula
- 2.1 The simple pendulum
- 2.2 The Foucault pendulum
- 2.3 The conical pendulum
- 3 References
- 4 See also
History[edit]
The history of the pendulum began when Galileo Galilei timed the period of a swinging lamp in Pisa cathedral using his pulse. He found that the period did not appear to change and believed it could be used to make a clock.[1] A pendulum was used to make a clock for the first time in 1656 by Christiaan Huygens.[2] Pendulum based clocks remained the most accurate time keeping devices until the 1930s when quartz clocks were developed.
Physics of Pendula[edit]
When the bob of the pendulum is at its lowest point, the pendulum is in equilibrium and is does not move. If the bob is moved slightly and released, the force of gravity acts on the pendulum trying to restore it to equilibrium and the pendulum will oscillate about this point. Despite the motion of a pendulum appearing to be very simple, the equation of motion for a particular pendulum cannot often be found exactly. Sometimes they can be expressed in terms of infinite series, otherwise approximations or numerical simulations using computers are used instead.
The simple pendulum[edit]
An example of an approximation is that of the simple pendulum. Here, a massless rod is used to connect the bob to its pivot, the bob is assumed to be a point particle and friction is neglected. The amplitude of the pendulum is the angle θ between the rod and the vertical and can be used to write an equation describing the motion of the pendulum:
where g is the acceleration due to gravity and l is the length of the pendulum. Even this equation cannot be solved exactly and a further approximation can be made: that the amplitude of the pendulum is small (around a few degrees). Therefore, 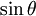 can be replaced with just θ meaning that the pendulum undergoes simple harmonic motion. The period can then be found as:
can be replaced with just θ meaning that the pendulum undergoes simple harmonic motion. The period can then be found as:
Interestingly, this means that for oscillations with small amplitudes, the period does not depend on the amplitude. In general, this is not true and it increases for larger amplitudes.
The Foucault pendulum[edit]

The Foucault pendulum consists of a heavy mass hung from a long line. It is allowed to swing in only a single plane. As it oscillates, the earth rotates beneath it causing the plane of oscillation to change and so it is evidence that the earth rotates.
The conical pendulum[edit]
The conical pendulum is a system that can be solved exactly. The bob follows a circular path in a horizontal plane and so performs circular motion.
References[edit]
- ↑ 1.0 1.1 Pendulum. Britannica.com. Retrieved on 2019-07-25.
- ↑ History of the Pendulum Clock. theclockdepot.com (2010-07-15). Retrieved on 2019-07-25.
See also[edit]
Clocks
Simple harmonic motion
Categories: [Physics] [Mechanics]
↧ Download as ZWI file | Last modified: 02/05/2023 22:31:10 | 22 views
☰ Source: https://www.conservapedia.com/Pendulum | License: CC BY-SA 3.0
 ZWI signed:
ZWI signed: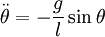
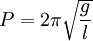
 KSF
KSF