Convergence

In mathematics convergence of an infinite series occurs when,

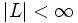for a finite number, .^[1] The terms in the limit are known as partial sums. If the partial sums approach or , the series is said to diverge. If the partial sums do not approach a single value, finite or infinite, then the series is said to have no limit.

Convergence of the series will occur only if (),

However, there is not one unique convergence condition (if or ).

Types of Convergence[edit]

A series is said to converge absolutely if the limit

If this limit holds for but not for , then the series is said to converge conditionally. If a series converges absolutely, then the series, , must also converge.

Real series convergence[edit]

There are many test for checking whether a series converges. A particularly important class of series are power series which have the form,

D'Alembert's Ratio Test[edit]

D'Alembert's ratio test states that for the limit:

the series will converge if L<1.^[2] if L>1 the series diverges and if L=0 the test is inconclusive and an alternative test must be used.

Alternating Series convergence[edit]

An alternating series is of the form,

This will converge if .

Cauchy's Root test[edit]

Cauchy's root test states that the limit:

can be used to test convergence.^[3] If:

• L<1, then the series converges absolutely and so must converge
• L>1, then the series diverges
• L=0, then the series may converge or diverge, another test must be used.

Limit Comparison Test[edit]

The limit comparison test allows one to test one series, , for convergence by comparing it to another series, , that is known to converge or diverge.^[4] This test is only valid if all terms in the two series are positive. It states that if the limit

is finite and then converges if converges or diverges if diverges.

Integral Test[edit]

Suppose we have a function, for which . Then if the limit:

exists, then the series must converge. If the integral cannot be evaluated, then the series diverges.^[5] This forms a very powerful technique for testing convergence. Furthermore, if the limit does exist, then upper and lower bounds for the series can be found:

where n₀ is the starting point of the series. As an example, consider the harmonic series, . Evaluating integral using we get:

The first natural logarithm goes to infinity as N goes to infinity. So although each term get smaller and smaller, the series diverges.

Intervals of convergence[edit]

The interval of convergence, also known as the radius of convergence, describes the range of values for which an infinite series converges.^[6] For real series this is an interval or region on the number line and can be expressed in the form a<x<b. As complex numbers have two components, this interval is transforms from a 1 dimensional line to the 2 dimensional area of a circle. Depending on the series, the interval of convergence may include some numbers, all numbers or no numbers. For example, the exponential function can be written as a power series:

This series converges for all x, real or complex. The binomial expansion of the function (1+x)^-1 is:

and only converges for |x|<1.

References[edit]

See also[edit]

• Series (mathematics)